[컴퓨터 구조] 2. 데이터

0과 1로 숫자를 표현하는 방법

[ 정보 단위 ]

컴퓨터는 0과 1로 모든 정보를 표현하고 0과 1로 표현된 정보만을 이해할 수 있다. 

 

비트(b) -> 0과 1을 나타내는 가장 작은 정보 단위. n비트는 2^n가지의 정보를 표현할 수 있다.

바이트(B) -> 8개의 1비트를 묶은 단위. 2^8(256)개의 정보를 표현할 수 있다.

킬로바이트(KB) -> 1000개의 1바이트를 묶은 단위.

메가바이트(MB) -> 1000개의 킬로바이트를 묶은 단위.

기가바이트(GB) -> 1000개의 메가바이트를 묶은 단위.

테라바이트(TB) -> 1000개의 기가바이트를 묶은 단위.

 

비트(b) < 바이트(B) < 킬로바이트(KB) < 메가바이트(MB) < 기가바이트(GB) < 테라바이트(TB) < 페타바이트(PB) < 엑사바이트(EB) < 제타바이트(ZB) < 요타바이트(YB) < 론나바이트(RB) < 퀘타바이트(QB)

 

[ 이진법 ]

수학에서 0과 1만으로 모든 숫자를 표현하는 방법. 아래 그림과 같이 숫자가 1을 넘어가는 시점에 자리 올림을 하여 0과 1, 두 개의 숫자만으로 모든 수를 표현한다.

 

즉, 우리는 일상적으로 십진수를 사용하지만, 0과 1밖에 모르는 컴퓨터에 어떤 숫자를 알려 주려면 십진수가 아닌 이진수로 알려주어야 한다. 또한, 일반적으로 십진수인지 이진수인지 구분하기 위해 이진수는 숫자 뒤에 (2)를 붙인다.

 

[ 이진수의 음수 표현 ]

십진수는 음수를 표현할 땐 단순히 숫자 앞에 마이너스 부호를 붙이면 그만이다. ex) -1, -3, -5. 하지만, 이진수는 컴퓨터가 0과 1만 이해할 수 있기 때문에 마이너스 부호를 사용하지 않고 0과 1만으로 음수를 표현해야 한다.

 

0과 1만으로 음수를 표현하는 방법 중 가장 널리 사용하는 방법은 2의 보수를 구해 이 값을 음수로 간주하는 방법이다. 2의 보수의 사전적 의미는 '어떤 수를 그보다 큰 2^n에서 뺀 값'을 의미한다. ex) 11(2)의 보수는 11(2)보다 큰 2^n, 즉 100(2)에서 11(2)를 뺀 01(2)가 되는 것이다.

 

 

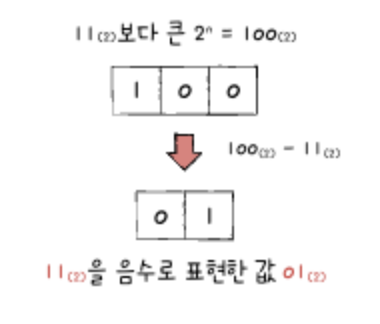
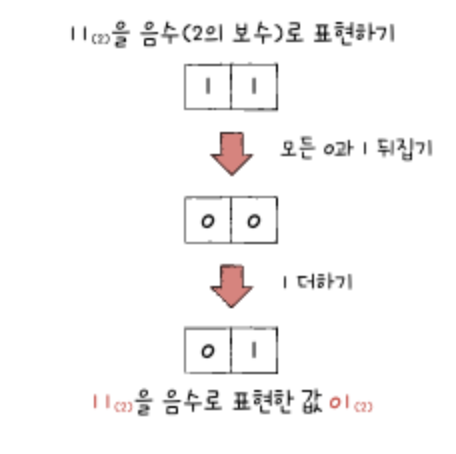
하지만, 굳이 이렇게 사전적 의미로 어렵게 이해할 필요는 없다. 2의 보수를 매우 쉽게 표현하자면 '모든 0과 1을 뒤집고, 거기에 1을 더한 값'으로 이해하면 된다. ex) 예를 들면, 11(2)의 모든 0과 1을 뒤집으면 00(2)이고 거기에 1을 더한 값은 01(2)가 된다.

 

또 하나의 예시로 들면, 1011(2)의 음수를 구하면 0101(2)이다. (모든 0과 1을 뒤집고 1을 더하면)

검증하기위해 음수를 두번 구하면 처음의 1011(2)로 나오니 아래 그림처럼 구할 수 있다.

 

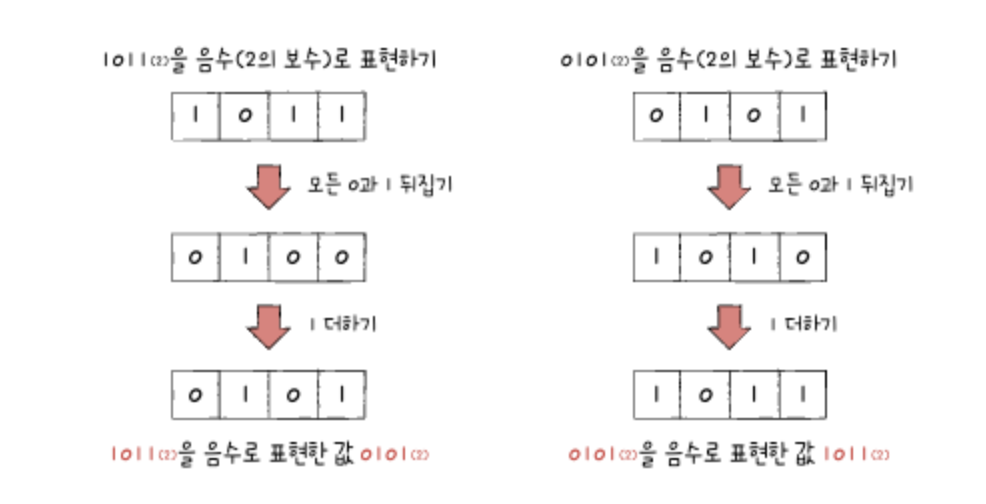
그런데, 위와 같은 경우에는 '-1011(2)를 표현하기 위한 음수 값 0101(2)와 십진수 5를 표현하기 위한 0101(2)가 똑같이 생겼는데, 이진수만 보고 음수인지 양수인지 어떻게 구분할 수 있을까?'에 대한 의문이 있을 수 있다.

 

실제로 이진수만 봐서는 이게 음수인지 양수인지 구분하기 어렵다. 그래서 컴퓨터 내부에서 어떤 수를 다룰 때는 이 수가 양수인지 음수인지를 구분하기 위해 플래그(flag)를 사용한다.

 

플래그는 쉽게 말해 부가 정보이다. 컴퓨터 내부에서 어떤 값을 다룰 때 부가 정보가 필요한 경우 플래그를 사용한다.(플래그에 대한 내용은 4번째 포스트에서 다룰 예정) 지금은 컴퓨터 내부에서 숫자들은 '양수' 혹은 '음수'가 적혀 있는 표시를 들고 다니므로 컴퓨터가 부호를 헷갈릴 필요는 없다 정도로 생각하면 된다.

 

[ 십육진법 ]

이진법을 이용해 0과 1만으로 모든 숫자를 표현할 수 있고, 하나의 이진수는 하나의 비트로 나타낼 수 있기에 이진법을 이용하면 컴퓨터가 이해하는 숫자 정보를 직접적으로 표현할 수 있다.

 

하지만, 이진법은 0과 1만으로 모든 숫자를 표현하다 보니 숫자의 길이가 너무 길어진다는 단점이 있다. 그래서 데이터를 표현할 때 십육진법도 자주 사용한다.

 

십육진법 -> 수가 15를 넘어가는 시점에 자리 올림을 하는 숫자 표현 방식이다. 십진수 10, 11, 12, 13, 14, 15는 십육진법 체계에서는 A, B, C, D, E, F로 표기한다.

 

십육진수는 숫자 앞에 0x를 붙여 구분한다. (ex. 0x15)

 

이 십육진법을 굳이 사용하는 이유는 이진수를 십육진수로, 십육진수를 이진수로 변환하기 쉽기 때문이다.

 

[ 십육진수를 이진수로 변환하기 ]

십육진수는 한 글자당 열여섯 종류의 숫자를 표현할 수 있다. 즉, 4비트가 필요하다.

 

십육진수를 이진수로 변환하는 간편한 방법 중 하나는 십육진수 한 글자를 4비트의 이진수로 간주하는 방법이다. 즉, 십육진수를 이루고 있는 각 글자를 따로따로 이진수로 변환하고 그것들을 그대로 이어 붙이면 십육진수의 이진수가 변환된다. 예를 들면, 1A2B(16)이라는 십육진수가 있을 때, 각 숫자 1(16), A(16), 2(16), B(16)를 이진수로 표현하면 0001(2), 1010(2), 0010(2), 1011(2)이다. 이 숫자를 그대로 이어 붙인 값, 즉 00001101000101011(2)이 1A2B(16)를 이진수로 표현한 값이다.

[ 이진수를 십육진수로 변환하기 ]

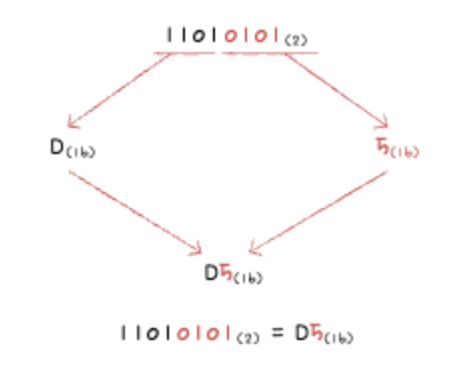
반대로 이진수를 십육진수로 변환할 때는 이진수 숫자를 네 개씩 끊고, 끊어 준 네 개의 숫자를 하나의 십육진수로 변환한 뒤 그대로 이어 붙이면 된다. 예를 들어 11010101(2)라는 이진수를 네개씩 끊으면 1101(2), 0101(2) 이고 십육진수로 바꾸면 D(16), 5(16)이므로 D5(16)가 십육진수로 변환한 수이다.

 

0과 1로 문자를 표현하는 방법

[ 문자 집합과 인코딩 ]

0과 1로 문자를 표현하는 방법에 대해 알아보기 전에 알아야 할 세가지 용어가 있다. 바로 문자 집합, 인코딩, 디코딩이다.

 

문자 집합 -> 컴퓨터가 인식하고 표현할 수 있는 문자의 모음. 컴퓨터는 문자 집합에 속해 있는 문자를 이해할 수 있고, 반대로 문자 집합에 속해 있지 않은 문자는 이해할 수 없다. 예를 들어, 문자 집합이 {a, b, c, d, e}인 경우 컴퓨터는 이 다섯 개의 문자는 이해할 수 있고, f, g는 이해할 수 없다.

 

문자 인코딩 -> 문자 집합에 속한 문자라고 해서 컴퓨터가 그대로 이해할 수 있는 것은 아니고 문자를 0과 1로 변환해야 비로소 컴퓨터가 이해할 수 있는데, 이 변환 과정을 문자 인코딩이라고 한다. 인코딩 후 0과 1로 이루어진 결과 값이 문자 코드가 된다.

 

문자 디코딩 -> 인코딩의 반대 과정으로, 0과 1로 이루어진 문자 코드를 사람이 이해할 수 있는 문자로 변환하는 과정이다.

 

정리하면 컴퓨터가 인식할 수 있는 문자들의 모음은 문자 집합, 이 문자들을 컴퓨터가 이해할 수 있는 0과 1로 변환하는 과정을 인코딩, 반대로 0과 1로 표현된 문자 코드를 사람이 읽을 수 있는 문자로 변환하는 과정을 디코딩이라고 한다.

 

[ 아스키 코드 ]

아스키는 초창기 문자 집합 중 하나로, 영어 알파벳과 아라비아 숫자, 그리고 일부 특수 문자를 포함한다. 아스키 문자 집합에 속한 문자들은 각각 7비트로 표현되며, 7비트로 표현할 수 있는 정보의 가짓수는 2^7개로, 총 128개의 문자를 표현할 수 있다.

 

아스키 문자들은 0부터 127까지 총 128개의 숫자 중 하나의 고유한 수에 일대일로 대응된다. 아스키 문자에 대응된 고유한 수를 아스키 코드라고 한다. 이 아스키 코드를 이진수로 표현함으로써 아스키 문자를 0과 1로 표현할 수 있다. 아스키 문자는 이렇게 아스키 코드로 인코딩 된다.

 

예를 들면, 'A'는 십진수 65로 인코딩 되고, 'a'는 십진수 97로, 특수 문자 !는 십진수 33으로 인코딩된다.

 

이렇게 아스키 코드는 매우 간단하게 인코딩된다는 장점이 있지만, 단점도 있다. 바로 한글과 아스키 문자 집합외에 문자, 특수문자도 표현할 수 없다. 근본적으로 아스키 문자 집합에 속한 문자들은 7비트로 표현하기 때문에 128개보다 많은 문자를 표현하지 못하기 때문이다. 그래서 아스키 코드에 1비트를 추가한 8비트의 확장 아스키가 등장했다.

 

그래서 한국을 포함한 영어권 외의 나라들은 자신들의 언어를 0과 1로 표현할 수 있는 고유한 문자 집합과 인코딩 방식이 필요하다 생각했기 때문에 이러한 이유로 등장한 한글 인코딩 방식이 바로 EUC-KR이다.

 

[ EUC-KR ]

한글 인코딩을 이해하려면 한글의 특수성을 알아야 한다. 알파벳을 쭉 이어쓰면 단어가 되는 영어와는 달리, 한글은 초성, 중성, 종성의 조합으로 이루어져 있다.

 

-> 그래서 한글 인코딩에는 두 가지 방식. 완성형(한글 완성형 인코딩)과 조합형(한글 조합에 인코딩)이 존재한다.

 

완성형 인코딩 -> 초성, 중성, 종성의 조합으로 이루어진 완성된 하나의 글자에 고유한 코드를 부여하는 인코딩 방식이다. 예를 들어 '가'는 1, '나'는 2, '다'는 3, 이런식으로 인코딩하는 방식이다.

 

조합형 인코딩 -> 초성을 위한 비트열, 중성을 위한 비트열, 종성을 위한 비트열을 할당하여 그것들의 조합으로 하나의 글자 코드를 완성하는 인코딩 방식이다.

 

ECU-KR은 KS X 1001, KS X 1003이라는 문자 집합을 기반으로 하는 대표적인 완성형 인코딩 방식이다. 즉, ECU-KR 인코딩은 초성, 중성, 종성이 모두 결합된 한글 단어에 2바이트 크기의 코드를 부여한다.

 

ECU-KR 인코딩 방식으로 총 2,350개 정도의 한글 단어를 표현할 수 있다. 아스키 코드보다는 표현할 수 있는 문자가 많아졌지만, 사실 모든 한글 조합을 표현할 수 있을 정도로 많은 양은 아니다. ex) '뤩', '뛝' 같은 글자는 ECU-KR로 표현할 수 없다.

 

그래서 ECU-KR 인코딩을 사용하는 웹사트의 한글이 깨진다든지, ECU-KR 방식으로는 표현할 수 없는 이름으로 인해 은행, 학교 등에서 피해를 받는 사람이 생겨나기도 했다.

 

이러한 문제를 조금이나마 해결하기 위해 등장한 것이 CP949이다. CP949는 ECU-KR의 확장된 버전으로, ECU-KR로는 표현할 수 없는 더욱 다양한 문자를 표현할 수 있다. 다만, 이마저도 한글 전체를 표현하기에 넉넉한 양은 아니다.

 

[ 유니코드와 UTF-8 ]

ECU-KR 인코딩 덕분에 한국어 코드를 표현할 수 있게 되었지만, 모든 한글을 표현할 수 없다는 한계가 있다. 또한, 이렇게 언어별로 인코딩을 나라마다 해야 한다면 다국어를 지원하는 프로그램을 만들 때 각 나라 언어의 인코딩을 모두 알아야 하는 번거로움이 있다. 예를 들면, 한국어, 영어, 일본어, 중국어, 독일어를 지원하는 웹사이트가 있다면 이 웹사이트는 다섯 개 언어의 인코딩 방식을 모두 이해하고 지원해야 한다.

 

유니코드 -> ECU-KR보다 훨씬 다양한 한글을 포함하며 대부분 나라의 문자, 특수문자, 화살표나 이모티콘까지도 코드로 표현할 수 있는 통일된 문자 집합.  즉, 모든 언어를 아우르는 문자 집합과 통일된 표준 인코딩 방식이라 언어별로 인코딩하는 수고로움을 덜 수 있다. 유니코드는 현대 문자를 표현할 때 가장 많이 사용되는 표준 문자 집합이며, 문자 인코딩 세계에서 매우 중요한 역할을 하고 있다.

 

유니코드는 아스키 코드나 ECU-KR과 같이 부여된 값을 그대로 인코딩된 값으로 삼지 않고 이 값 다양한 방법으로 인코딩한다. ex) UTF-8, UTF-16, UTF-32

 

UTF-8 -> 통상 1바이트부터 4바이트까지의 인코딩 결과를 만들어낸다. 다시 말해 UTF-8로 인코딩한 값의 결과는 1바이트가 될 수도, 2바이트, 3바이트, 4바이트가 될 수도 있다.

References

혼자 공부하는 컴퓨터 구조 + 운영체제, 강민철 (2022)